ASCROM package documentation

Package dependencies
Atomic model ClimaticWaterDemand
1. Configuring a ClimaticWaterDemand Model
2. Details
Atomic model WaterFlows
1. Configuring a WaterFlows Model
2. Details
Atomic model IrrigationDemand
1. Configuring a IrrigationDemand Model
2. Details
Atomic model ActualIrrigation
1. Configuring a ActualIrrigation Model
2. Details
Atomic model Yield
1. Configuring a Yield Model
2. Details
Atomic model Pond
1. Configuring a Pond Model
2. Details
Atomic model IrrigationPriority
1. Configuring a IrrigationPriority Model
2. Details
Atomic model FarmIrrigationManager
1. Configuring a FarmIrrigationManager Model
2. Details
Annexe

Package dependencies

List of required external packages (with link to distribution when available).

vle.discrete-time

Atomic model ClimaticWaterDemand

The ClimaticWaterDemand model (using extension class DiscreteTimeDyn) calculates the daily potential evapotranspiration. This calculation is split in two parts: calculation of the potential crop transpiration and calculation of the potential soil evaporation. We use the generic approach based on Kcb (basal crop coefficient) and proposed by FAO method, to estimate the potential transpiration. We calculate a coefficient Ke to estimate the potential evaporation of soil. This model also handles the dynamic of crop growth (growth of roots ).

Configuring a ClimaticWaterDemand Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : ClimaticWaterDemand

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
SoilDepth	double	[x]	soil depth [double] [m]
REW1	double	[x]	soil surface layer readily evaporable water. Cumulative depth of evaporation (depletion) at the end of stage 1 [mm] see Table 4
REW2	double	[x]	soil deep layer readily ?? water. Cumulative depth of ?? (depletion) at the end of stage 1 [mm] see Table 4
fw	double	[x]	average fraction of soil surface wetted by irrigation or light rainfalls (i.e rain < Rain_Threshold) [0.01 - 1]. If heavy rainfall, fw=1. See Table Table 4
fw_Rain_Threshold	double	[x]	Rain threshold where fw=1.
Failure_Option	int	[x]	Choose crop failure option {0:none, 1:water, 2:yield, 3:water&yield, 4:water\|yield}.
few_parameter	double	[] (default=1)	reference parameter for few computation.
isDrip	boolean	[] (default=False)	Drip option for few computation.

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

ET0 : Reference crop evapotranspiration (We recommend to use values calculated by the Penman Monteith equation as it is done in FAO approach) (mm.d^-1) (double) (sync)
WC_R1 : soil surface layer water content (mm) (double) (nosync)
WC_R2 : soil deep layer water content (mm) (double) (nosync)
RHmin : daily air minimal relative humidity (%) (double) (sync)
u2 : daily wind speed at 2m (m.s^-1) (double) (sync)
Rain : daily rain (mm.d-1) (double) (sync)
Is_Day_Without_Irrigation : detect if day has no irrigation where it should have (bool) (double) (sync)
YieldFraction : Yield/Yield_max fraction (-) (double) (nosync)
kcb_interp : kcb interpolation (-) (double) (sync)
kcini_interp : kcini interpolation (-) (double) (sync)
kcmid_interp : kcmid interpolation (-) (double) (sync)
h_interp : h interpolation (m) (double) (sync)
MaxDepthRoots_interp : MaxDepthRoots interpolation (m) (double) (sync)
Rain_Threshold_To_Reset_Days_Without_Water : water threshold for water deficit counter. (mm) (double) (sync)
Lethal_Threshold_Days_Without_Water : number of days of water deficit after which the crop is failed. (days) (double) (sync)
Lethal_Threshold_YieldFraction : Crop YieldFraction threshold for crop failure. (-) (double) (sync)
NoFailurePeriod : Minimum duration since sowing before failure based on yield. (days) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

Kcb : Basal crop coefficient after specific adjustment in climates. Kcb+Ke<1,4. Kcb-Kcmin>= 0,01 (-) (double)
h : the mean plant height during the mid or late season stage (m) (double)
MaxDepthRoots : Maximum depth of roots (m) (double)
kcini : () (double)
kcmid : () (double)
Ke : Soil evaporation coefficient. Kcb+Ke<1,4 (-) (double)
RootDepth : Crop root depth (m) (double)
Max_transp : Daily maximal crop transpiration (mm.d-1) (double)
Max_evap : Daily maximal soil evaporation from soil surface layer (mm.d^-1) (double)
PET: Crop evapotranspration under standard conditions using a dual crop coefficient, one for transpiration (Kcb) and one for soil evaporation (Ke). (mm.d^-1) (double)
Kcmax : Maximum value of Kc following rain or irrigation. Kcmax [1,05 ; 1,3] (-) (double)
Kr1 : Soil evaporation reduction coefficient. (-) (double)
Kr2 : Soil ?? reduction coefficient. (-) (double)
fc : Average soil fraction covered (or shaded) by vegetation [0.01 - 1] - see Table Table 3 (-) (double)
few : Exposed and wetted soil fraction (-) (double)
Days_Without_Water : number of consecutive days with water deficit (d) (double)
Is_Failure_From_WaterSupply : detect if water deficit threshold has been reached for the current crop (bool) (double)
Is_Failure_From_YieldFraction : detect if crop YieldFraction threshold has been reached for the current crop (bool) (double)
Is_Failure : detect if crop has failed (bool) (double)
Failure_counter : total number of failure (int) (double)
Days_Since_Sowing : number of days since sowing (int) (double)

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/ClimaticWaterDemand : set all parameters with default values

Details

State variables equations

Calculation of Kcb

Kcb(t) : Reference value of Kcb (after climatic correction). The calculation is first based on the linear interpolation from a set of pairs (Kc_params). In the FAO approach, the calculation is based on three pairs of values: Kcini, Kcmid, Kcend, provided in Table 1 (Annexe), and average stage durations for each crop, by climate are provided in Table 5 (Annexe).
We then also add a potential failure process based on consecutive days with water deficit (Days_Without_Water) and/or crop yield fraction (YieldFraction).

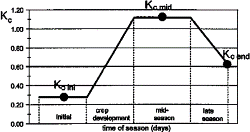
Kc evolution

\[ Is\_Failure\_From\_WaterSupply(t) = Is\_Failure\_From\_WaterSupply(t-1) | (Days\_Without\_Water(t-1) \geq Lethal\_Threshold\_Days\_Without\_Water(t)) \label{eq:Is_Failure_From_WaterSupply}\]

\[ Is\_Failure\_From\_YieldFraction(t) = Is\_Failure\_From\_YieldFraction(t-1) | (YieldFraction(t-1) \leq Lethal\_Threshold\_YieldFraction(t) \text{&} Days\_Since\_Sowing(t-1) > NoFailurePeriod(t)) \label{eq:Is_Failure_From_YieldFraction}\]

\[ Is\_Failure(t)=\left\{ \begin{array}{@{}ll@{}} (Kcb\_interp(t)>0) \text{&} Is\_Failure\_From\_WaterSupply(t), & \text{if}\ Failure\_Option=1 \\ (Kcb\_interp(t)>0) \text{&} Is\_Failure\_From\_YieldFraction(t), & \text{else if}\ Failure\_Option=2 \\ (Kcb\_interp(t)>0) \text{&} Is\_Failure\_From\_WaterSupply(t) \text{&} Is\_Failure\_From\_YieldFraction(t), & \text{else if}\ Failure\_Option=3 \\ (Kcb\_interp(t)>0) \text{&} (Is\_Failure\_From\_WaterSupply(t) \text{|} Is\_Failure\_From\_YieldFraction(t)), & \text{else if}\ Failure\_Option=4 \\ False, & \text{otherwise} \\ \end{array}\right. \label{eq:Is_Failure}\]

\[ Failure\_counter(t)=\left\{ \begin{array}{@{}ll@{}} Failure\_counter(t-1) + 1, & \text{if}\ (Is\_Failure(t-1)=0) \text{&} (Is\_Failure(t)=1) \\ Failure\_counter(t-1), & \text{otherwise} \\ \end{array}\right. \label{eq:Failure_counter}\]

\[ Days\_Without\_Water(t)=\left\{ \begin{array}{@{}ll@{}} Days\_Without\_Water(t-1), & \text{if}\ Is\_Failure(t) \\ Days\_Without\_Water = Days\_Without\_Water(t-1) + 1, & \text{else if}\ Is\_Day\_Without\_Water \\ 0, & \text{otherwise} \end{array}\right. \label{eq:Days_Without_Water}\]
with
\(Is\_Day\_Without\_Water = (Kcb\_interp(t)>0) \text{&} ((Rain(t)<Rain\_Threshold\_To\_Reset\_Days\_Without\_Water(t)) \text{&} (Is\_Day\_Without\_Irrigation(t))\)

\[ Kcb(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ Kcb\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:Kcb}\]

\[ h(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ h\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:h}\]

\[ MaxDepthRoots(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ MaxDepthRoots\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:MaxDepthRoots}\]

\[ kcini(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ kcini\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:kcini}\]

\[ kcmid(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ kcmid\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:kcmid}\]

\[ Days\_Since\_Sowing(t)=\left\{ \begin{array}{@{}ll@{}} Days\_Since\_Sowing(t-1) + 1, & \text{if}\ kcb(t) > 0 \\ 0, & \text{otherwise} \end{array}\right. \label{eq:Days_Since_Sowing}\]

Calculation of Ke

This requires the prior calculation of different variables or parameters: Kcmax, AWC1, Kr …

Kcmax: represents an upper limit on evaporation and transpiration from the cropped surface. Kcmax ranges from about 1.05 to 1.30
\[ Kcmax(t)=\max\left( \begin{array}{@{}ll@{}} 1.2 + (0.04 * (u2(t) -2) -0.004 * (RHmin(t) -45)) * (h(t)/3)^{0.3} \\ Kcb(t) + 0.05 \end{array}\right) \label{eq:Kcmax }\]

Kr1: Soil evaporation and transpiration reduction coefficient. [dimensionless] [double]
Soil evaporation and transpiration from the exposed soil can be assumed to take place in two stages: an energy limiting stage, and a falling rate stage. During Stage 1, the soil surface remains wet and evaporation and transpiration are predicted to occur at the maximum rate limited only by energy availability at the soil surface and therefore, Kr1=1. As the soil surface dries, the evaporation and transpiration rate decreases below the potential rate, and Kr1 becomes less than one. Kr1 becomes zero when no water is left for evaporation and transpiration in the top soil reservoir.

\[ Kr1(t)=\min\left( \begin{array}{@{}ll@{}} 1 \\ \frac{WC\_R1(t-1)}{REW1} \end{array}\right) \label{eq:Kr1}\]

Kr2: Soil transpiration reduction coefficient. [dimensionless] [double]
Soil transpiration from the soil deep reservoir can be assumed to take place in two stages: an energy limiting stage, and a falling rate stage. During Stage 1, the soil remains wet and transpiration is predicted to occur at the maximum rate limited only by energy availability at the soil and therefore, Kr2=1. As the soil surface dries, the transpiration rate decreases below the potential rate, and Kr2 becomes less than one. Kr2 becomes zero when no water is left for transpiration in the soil deep reservoir. \[ Kr2(t)=\min\left( \begin{array}{@{}ll@{}} 1 \\ \frac{WC\_R2(t-1)}{REW2} \end{array}\right) \label{eq:Kr2}\]

1 - fc : average exposed soil fraction not covered (or shaded) by vegetation [0.01 - 1] - see Table Table 3
fc can also be estimated using the relationship.
\[fc(t) = (\frac{Kcb(t) - Kcini(t)}{Kcmax(t) - Kcini(t)})^{1 + 0.5*h} \label{eq:fc}\]
Remark : fc()=0 when kcb()=0

few : Exposed and wetted soil fraction
\[few(t)=\left\{ \begin{array}{@{}ll@{}} \max\left( \begin{array}{@{}ll@{}} 1 - 2/3 * fc(t) \\ 0 \end{array}\right) * fw, & \text{if}\ isDrip \\ \min\left( \begin{array}{@{}ll@{}} \max\left( \begin{array}{@{}ll@{}} 1 - few\_parameter * fc(t) \\ 0 \end{array}\right) \\ fw\_Rain \end{array}\right), & \text{otherwise} \end{array}\right. \label{eq:few}\] with \[fw\_Rain=\left\{ \begin{array}{@{}ll@{}} fw, & \text{if}\ Rain(t) < fw\_Rain\_Threshold \\ 1, & \text{otherwise} \end{array}\right. \]

Ke(t): Soil evaporation coefficient, Ke, describes the evaporation component of ETP. Where the topsoil is wet, following rain or irrigation, Ke is maximal, it only depends of the energy available for the evaporation process. Where the soil surface is dry, Ke is small and even zero when no water remains near the soil surface for evaporation.
\[Ke(t)=\min\left( \begin{array}{@{}ll@{}} Kr1(t) * (Kcmax(t) - Kcb(t)) \\ few(t) * Kcmax(t) \end{array}\right) \label{eq:Ke}\]

RootDepth(t): Depth of roots (m). (0 to MaxDepthRoots)
\[RootDepth(t)=\min\left( \begin{array}{@{}ll@{}} MaxDepthRoots(t) \\ SoilDepth \\ MaxDepthRoots(t) * Kcb(t)/Kcmid(t) \end{array}\right) \label{eq:RootDepth}\]

Max_transp(t) : Maximum transpiration
\[Max\_transp(t) = Kcb(t) * ET0(t) \label{eq:Max_transp}\]

Max_evap(t) : Maximum evaporation
\[Max\_evap(t) = Ke(t) * ET0(t) \label{eq:Max_evap}\]

PET(t): Potential Evapotranspiration
\[PET(t) = Max\_transp(t) + Max\_evap(t) \label{eq:PET}\]

Atomic model WaterFlows

The WaterFlows model (using extension class DiscreteTimeDyn) estimate water flows from climatic and irrigation demands and available pumping water.
The water available for the crop is provided by rain and irrigation (and soil stock).
The soil is splitted into a surface layer (where both soil evaporation and a fraction of the total crop transpiration can occur), and a deep layer where only remaining crop transpiration is possible.
The crop potential transpiration demand is splitted homogeneously among the 2 soil layers according to the RootDepth.
In the case of unsatisfied transpiration demand in the surface layer, the difference is added to the deep layer transpiration demand.

Configuring a WaterFlows Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : WaterFlows

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
CurveNumber	double	[x]	RunOff CurveNumber parameter (??)
Ia_SoilType_param	double	[x]	RunOff Ia parameter (??)
TH1	double	[x]	soil surface layer thickness (mm)
ThetaFC1	double	[x]	soil surface layer water content at field capacity (%)
ThetaWP1	double	[x]	soil surface layer water content wilting point (%)
BD1	double	[x]	soil surface layer bulk density (-)
TH2	double	[x]	soil deep layer thickness (mm)
ThetaFC2	double	[x]	soil deep layer water content at field capacity (%)
ThetaWP2	double	[x]	soil deep layer water content wilting point (%)
BD2	double	[x]	soil deep layer bulk density (-)

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

Rain : daily rain (mm.d-1) (double) (sync)
ActualIrrigation : water supply (mm.d-1) [double] (sync)
Max_evap : daily maximal soil evaporation from soil surface layer (mm.d-1) (double) (sync)
Max_transp : daily maximal crop transpiration (mm.d-1) (double) (sync)
RootDepth : crop root depth (m) (double) (sync)
few : Exposed and wetted soil fraction (-) (double) (sync)
fc : Average soil fraction covered (or shaded) by vegetation [0.01 - 1] - see Table Table 3 (-) (double) (sync)
Kr1 : Soil evaporation reduction coefficient. (-) (double) (sync)
Kr2 : Soil ?? reduction coefficient. (-) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

max_trans_R1 : daily maximal crop transpiration from soil surface layer (mm.d-1) (double)
max_trans_R2 : daily maximal crop transpiration from soil deep layer (mm.d-1) (double)
actual_evap : daily soil surface actual evaporation (mm.d-1) (double)
actual_transp_R1 : daily crop actual transpiration from soil surface layer (mm.d-1) (double)
actual_transp_R2 : daily crop actual transpiration from soil deep layer (mm.d-1) (double)
actual_transp : daily crop actual transpiration (mm.d-1) (double)
Irrigation : daily actual irrigation (mm.d-1) (double)
RunOff : daily soil surface runoff (mm.d-1) (double)
I_R1 : daily soil surface layer infiltration (mm.d-1) (double)
I_R2 : daily soil deep layer infiltration (mm.d-1) (double)
Drain : daily soil deep layer drainage (mm.d-1) (double)
WC_R1 : soil surface layer water content (mm) (double)
WC_R2 : soil deep layer water content (mm) (double)
WCtmp_R1 : temporary soil surface layer water content (after gravitational infiltrations and before evapotranspiration) (mm) (double)
WCtmp_R2 : temporary soil deep layer water content (after gravitational infiltrations and before evapotranspiration) (mm) (double)
stress_index : crop water stress index (-) (double)
DailyBalanceControl : control for daily water budget checking (should always be 0) (m) (double)

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/WaterFlows : set all parameters with default values

Details

State variables equations

\[RunOff(t)=\left\{ \begin{array}{@{}ll@{}} \frac{(Rain(t) - Ia)^2}{Rain(t) - Ia - S}, & \text{if}\ Rain(t) > Ia\\ 0, & \text{otherwise} \end{array}\right. \label{eq:RunOff}\]
with
\(S = \frac{25400}{CurveNumber} - 254\)
and
\(Ia = Ia\_SoilType\_param * S\)

\[I\_R1(t)=\max\left( \begin{array}{@{}ll@{}} 0. \\ Rain(t) + ActualIrrigation(t) - RunOff(t) \end{array}\right) \label{eq:I_R1}\]

\[I\_R2(t)=\max\left( \begin{array}{@{}ll@{}} 0. \\ WC\_R1(t-1) + I\_R1(t) - AWC1 \end{array}\right) \label{eq:I_R2}\]
with
\(AWC1 = (ThetaFC1 - ThetaWP1) * BD1 * TH1\)

\[Drain(t)=\max\left( \begin{array}{@{}ll@{}} 0. \\ WC\_R2(t-1) + I\_R2(t) - AWC2 \end{array}\right) \label{eq:Drain}\]
with
\(AWC2 = (ThetaFC2 - ThetaWP2) * BD2 * TH2\)

\[WCtmp\_R1(t) = WC\_R1(t-1) + I\_R1(t) - I\_R2(t) \label{eq:WCtmp_R1}\]

\[WCtmp\_R2(t) = WC\_R2(t-1) + I\_R2(t) - Drain(t) \label{eq:WCtmp_R2}\]

\[max\_trans\_R1(t)=\min\left( \begin{array}{@{}ll@{}} 1. \\ \frac{TH1}{RootDepth(t)*1000} \end{array}\right) * Max\_transp(t) \label{eq:max_trans_R1}\]

\[max\_trans\_R2(t)=\max\left( \begin{array}{@{}ll@{}} 0. \\ \frac{RootDepth(t)*1000 - TH1}{RootDepth(t)*1000} \end{array}\right) * Max\_transp(t) \label{eq:max_trans_R2}\]

\[actual\_evap(t)=\left\{ \begin{array}{@{}ll@{}} Max\_evap(t), & \text{if}\ Max\_evap(t) + max\_trans\_R1(t) \le WCtmp\_R1(t) or Max\_evap(t)<few(t) * WCtmp\_R1(t)\\ few(t) * WCtmp\_R1(t), & \text{otherwise} \end{array}\right. \label{eq:actual_evap}\]

\[actual\_transp\_R1(t)=\left\{ \begin{array}{@{}ll@{}} max\_trans\_R1(t) * Kr1(t), & \text{if}\ Max\_evap(t) + max\_trans\_R1(t) \le WCtmp\_R1(t) \\ fc(t) * \min\left( \begin{array}{@{}ll@{}} max\_trans\_R1(t) * Kr1(t) \\ WCtmp\_R1(t) \end{array}\right), & \text{otherwise} \end{array}\right. \label{eq:actual_transp_R1}\]

\[actual\_transp\_R2(t)= \min\left( \begin{array}{@{}ll@{}} Kr2(t) * (max\_trans\_R1(t) - actual\_transp\_R1(t) + max\_trans\_R2(t)) \\ WCtmp\_R2(t) * fracRoot\_R2 \end{array}\right) \label{eq:actual_transp_R2}\]
with
\[fracRoot\_R2=\max\left( \begin{array}{@{}ll@{}} 0. \\ \frac{RootDepth(t)*1000 - TH1}{TH2} \end{array}\right) \label{eq:fracRoot_R2}\nonumber\]

\[actual\_transp(t) = actual\_transp\_R1(t) + actual\_transp\_R2(t) \label{eq:actual_transp}\]

\[WC\_R1(t)=\min\left( \begin{array}{@{}ll@{}} AWC1 \\ WCtmp\_R1(t) - actual\_transp\_R1(t) - actual\_evap(t) \end{array}\right) \label{eq:WC_R1}\]

\[WC\_R2(t)=\min\left( \begin{array}{@{}ll@{}} AWC2 \\ WCtmp\_R2(t) - actual\_transp\_R2(t) \end{array}\right) \label{eq:WC_R2}\]

\[stress\_index = \frac{actual\_transp(t)}{Max\_transp(t)} \label{eq:stress_index}\]

\[DailyBalanceControl(t) = \Delta WC(t) - Rain(t) - ActualIrrigation(t) + RunOff(t) + Drain(t) + actual\_evap(t) + actual\_transp\_R1(t) + actual\_transp\_R2(t) \label{eq:DailyBalanceControl}\]
with
\(\Delta WC(t) = (WC\_R1(t) + WC\_R2(t)) - (WC\_R1(t-1) + WC\_R2(t-1))\)

De(t) Cumulative depth of evaporation (depletion) from the soil surface layer after a day with “heavy precipitation” [m],

FAO equation : \(De(t) = max(0, De(t-1) -(P(t)-R(t)) - I(t)/fw + Max\_evap(t)/few + AWC1(t) + DPe(t))\) combined with
\(De(t) = AWC1 - WC\_R1(t)\)

→

\(AWC1 - WC\_R1(t) = max(0, AWC1 - WC\_R1(t-1) -(P(t)-R(t)) - I(t)/fw + Max\_evap(t)/few + AWC1(t) + DPe(t))\)

→

\(-WC\_R1(t) = max(-AWC1, - WC\_R1(t-1) -(P(t)-R(t)) - I(t)/fw + Max\_evap(t)/few + AWC1(t) + DPe(t))\)

→

\(WC\_R1(t) = min(AWC1, WC_R1(t-1) + (P(t)-R(t)) + I(t)/fw - Max\_evap(t)/few - AWC1(t) - DPe(t))\) combined with
\(P(t)=Rain(t)\)
\(R(t)=RunOff(t)\)
\(I(t)=Irrigation(t)\)
\(DPe(t)=I\_R2(t)\)

→

\(WC\_R1(t) = min(AWC1, WC_R1(t-1) + (Rain(t)-RunOff(t)) + Irrigation(t)/fw - Max\_evap(t)/few - AWC1(t) - I\_R2(t))\)

to be compared to WaterFlow eq (combination of above eq for WC_R1, WCtmp_R1, I_R1) :

\[WC\_R1(t)=\min\left( \begin{array}{@{}ll@{}} AWC1 \\ WC\_R1(t-1) + Rain(t) + Irrigation(t) - RunOff(t) - I\_R2(t) - actual\_transp\_R1(t) - actual\_evap(t) \end{array}\right) \label{eq:WC_R1.2}\nonumber\]

Atomic model IrrigationDemand

The IrrigationDemand model (using extension class DiscreteTimeDyn) estimate daily irrigation demand.

Configuring a IrrigationDemand Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : IrrigationDemand

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
Rule_Strat	string	[x]	strategy option for irrigation rule (choose from {None, Rain_Threshold, SoilWaterContent_Threshold, CropWaterStress_Threshold})

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

Rain7days : cummulated rain over the last 7 days (mm.d-1) (double) (sync)
Irrigation7days : cummulated irrigation over the last 7 days (mm.d-1) (double) (nosync)
CropWaterStress : crop water stress index (-) (double) (nosync)
SoilWaterContent : soil water content (mm) (double) (nosync)
Is_Failure : detect if water deficit threshold has been reached for the current crop (bool) (double) (nosync)
IrrigationDose_interp : IrrigationDose interpolation (mm.d^-1) (double) (sync)
Rain_Threshold_interp : Rain_Threshold interpolation (mm) (double) (sync)
SoilWaterContent_Threshold_interp : SoilWaterContent_Threshold interpolation (mm) (double) (sync)
CropWaterStress_Threshold_interp : CropWaterStress_Threshold interpolation (-) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

IrrigationDemand : daily irrigation demand of the 1st subplot (mm.d^-1) (double)
IrrigationDose : irrigation amount to be applied (mm.d^-1) (double)
Rain_Threshold : Rain amount threshold for Rule_Strat=Rain_Threshold (mm) (double)
CropWaterStress_Threshold : Crop water stress threshold for Rule_Strat=CropWaterStress_Threshold (-) (double)
SoilWaterContent_Threshold : Soil water content threshold for Rule_Strat=SoilWaterContent_Threshold (mm) (double)

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/IrrigationDemand : set all parameters with default values

Details

State variables equations

By setting the value of parameter Rule_Strat the user is choosing one of the following irrigation strategy:

None: No particular restriction, irrigation happens ASAP
Rain_Threshold: Irrigation event start restricted by Rain7days and Irrigation7days daily inputs and using Rain_Threshold_params parameters
SoilWaterContent_Threshold: Irrigation event start restricted by SoilWaterContent daily inputs and using SoilWaterContent_Threshold_params parameters
CropWaterStress_Threshold Irrigation event start restricted by CropWaterStress daily inputs and using CropWaterStress_Threshold_params parameters

\[ IrrigationDose(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ IrrigationDose\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:IrrigationDose}\]

Depending on the Rule_Strat option choosed, a criterion might be used to decide if a new irrigation event should start. (see below the different options).

\[Irrigation\_Demand(t) = IrrigationDose(t) \label{eq:Irrigation_Demand}\]

Rule_Strat=Rain_Threshold

The cummulated rain over the last 7 days is compared to a threshold value

\[ Rain\_Threshold(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ Rain\_Threshold\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:Rain_Threshold}\]

\[ start\_rule=(Rain7days(t) + Irrigation7days(t-1) < Rain\_Threshold(t)) \label{eq:start_Rain_Threshold}\]

Rule_Strat=SoilWaterContent_Threshold

The soil water content is compared to a threshold value

\[ SoilWaterContent\_Threshold(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ SoilWaterContent\_Threshold\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:SoilWaterContent_Threshold}\]

\[ start\_rule=(SoilWaterContent(t-1) < SoilWaterContent\_Threshold(t)) \label{eq:start_SoilWaterContent_Threshold}\]

Rule_Strat=CropWaterStress_Threshold

The crop water stress index is compared to a threshold value (Remark : for the crop water stress index defined in the WaterFlows model 0 is max stress and 1 no stress)

\[ CropWaterStress\_Threshold(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ Is\_Failure(t) \\ CropWaterStress\_Threshold\_interp(t), & \text{otherwise} \end{array}\right. \label{eq:CropWaterStress_Threshold}\]

\[ start\_rule=(CropWaterStress(t-1) < CropWaterStress\_Threshold(t)) \label{eq:start_CropWaterStress_Threshold}\]

Atomic model ActualIrrigation

The ActualIrrigation model (using extension class DiscreteTimeDyn) estimate ….

Configuring a ActualIrrigation Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : ActualIrrigation

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
Irrig_Efficiency	double	[x]	fraction of irrigation water reaching soil surface.

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

Irrigation : daily irrigation applied (mm.d-1) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

ActualIrrigation : water supply (mm.d-1) [double]

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/ActualIrrigation : set all parameters with default values

Details

State variables equations

\[ActualIrrigation(t)= Irrigation(t) * Irrig\_Efficiency \label{eq:ActualIrrigation}\]

Atomic model Yield

The Yield model (using extension class DiscreteTimeDyn) estimate ….

Configuring a Yield Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : Yield

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

CropWaterStress : crop water stress index (-) (double) (sync)
Is_Failure : detect if crop has failed (bool) (double) (sync)
YieldMax : ?? (??) (double) (sync)
Ky : Yield response factor (-) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

StressReductionFactor : ?? (??) [double]
Yield : ?? (??) [double]
YieldFraction : ?? (??) [double]

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/Yield : set all parameters with default values

Details

State variables equations

\[StressReductionFactor(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ !Is\_Crop \\ \frac{StressReductionFactor(t-1)*(daycounter(t)-1) + CropWaterStress(t))}{daycounter(t)}, & \text{otherwise} \end{array}\right. \label{eq:StressReductionFactor}\]
with
\(Is\_Crop = ((YieldMax(t) > 0) \text{&} !Is\_Failure(t))\)
and
\(daycounter(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ !Is\_Crop \\ daycounter(t-1)+1, & \text{otherwise} \end{array}\right.\)

\[Yield(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ !Is\_Crop \\ \max\left( \begin{array}{@{}ll@{}} YieldMax(t) * (1. - Ky(t) * (1. - StressReductionFactor(t))) \\ 0. \end{array}\right), & \text{otherwise} \end{array}\right. \label{eq:Yield}\]

\[YieldFraction(t)=\left\{ \begin{array}{@{}ll@{}} 0, & \text{if}\ !Is\_Crop \\ Yield(t)/YieldMax(t), & \text{otherwise} \end{array}\right. \label{eq:YieldFraction}\]

Atomic model Pond

The Pond model (using extension class DiscreteTimeDyn) estimate the pond volume and water flows (Evaporation, percolation and overflow internal processes and potential refilling/extraction from/for external sources).

The shape of the pond is a reversed truncated pyramid with a rectangular shaped base :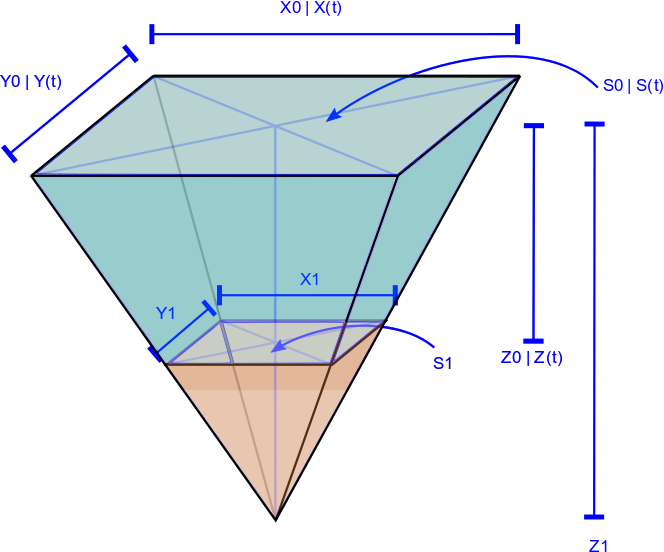

Configuring a Pond Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : Pond

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
X0	double	[x]	Pond surface Length (m)
Y0	double	[x]	Pond surface Width (m)
Z0	double	[x]	Pond depth (m)
fx	double	[x]	Shape coefficient for X dimension (must be positive) (m/m)
Evap_coeff	double	[x]	Pond evaporation reduction coefficient (??)
Percol_coeff	double	[x]	Pond percolation coefficient (??)
Init_Pond_Frac	double	[x]	Pond initial volume as a fraction of V0 (-)

Local parameters

The following are computed once from user parameters and then keep a fixed value during the simulation duration

Parameter name	Type	Description
fy	double	Shape coefficient for Y dimension (m/m)
S0	double	Pond surface area (m²)
X1	double	Pond bottom Length (m)
Y1	double	Pond bottom Width (m)
Z1	double	Pyramid Apex depth (m)
S1	double	Pond bottom area (m²)
V0	double	Pond total volume (m³)
V1	double	Trunk volume of the truncated pyramid (m³)

\[fy = \frac{Y0 * fx}{X0} \label{eq:fy}\]

\[S0 = X0 * Y0 \label{eq:S0}\]

\[X1 = X0 - fx * Z0 \label{eq:X1}\]

\[Y1 = Y0 - fy * Z0 \label{eq:Y1}\]

\[Z1 = \frac{X0}{fx} = \frac{Y0}{fy} \label{eq:Z1}\]

\[S1 = X1 * Y1 \label{eq:S1}\]

\[V0 = \frac{1}{3} * Z0 * (S0 + S1 + \sqrt{S0 * S1}) \label{eq:V0}\]

\[V1 = \frac{1}{3} * (Z1 - Z0) * (S0 + S1 + \sqrt{S0 * S1}) = \frac{1}{3} * (Z1 - Z0)^3 * fx * fy \label{eq:V1}\]

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

ET0 : Reference crop evapotranspiration (We recomend to use values calculated by the Penman Monteith equation as it is done in FAO approach) (mm.d^-1) (double) (sync)
Rain : daily rain (mm) (double) (sync)
RunOff : daily incoming surface runoff volume (m³) (double) (sync)
Pond_Irrigation : daily actual irrigation using pond water (m³) (double) (sync)
AvailableWater : daily available water for refilling the pond (m³) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

Evaporation : Pond daily surface Evaporation (m³) (double)
Percolation : Pond daily bottom Percolation (m³) (double)
Pump_water_refill : Pond daily Refill volume (m³) (double)
Pond_Overflow : Pond water overflow loss (m³) (double)
V : Pond water volume (m³) (double)
X : Pond water Length (m) (double)
Y : Pond water Width (m) (double)
S : Pond water area (m²) (double)
Z : Pond water height (m) (double)

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/Pond : set all parameters with default values

Details

State variables equations

\[Percolation(t) =\min\left( \begin{array}{@{}ll@{}} Z(t-1) * S1 * Percol\_coeff \\ V(t-1) + Rain(t) * S0 / 1000. + RunOff(t) - Pond\_Irrigation(t) \end{array}\right) \label{eq:Percolation}\]

\[Evaporation(t) =\min\left( \begin{array}{@{}ll@{}} ET0(t) * Evap\_coeff * S(t-1) / 1000 \\ V(t-1) - Percolation(t) + Rain(t) * S0 / 1000. + RunOff(t) - Pond\_Irrigation(t) \end{array}\right) \label{eq:Evaporation}\]

\[Pump\_water\_refill(t)=\min\left( \begin{array}{@{}ll@{}} V0 - \min\left( \begin{array}{@{}ll@{}} V0 \\ (V(t-1) + Rain(t) * S0 / 1000. + RunOff(t) - Pond\_Irrigation(t) - Evaporation(t) - Percolation(t)) \end{array}\right) \\ AvailableWater(t) \end{array}\right) \label{eq:Pump_water_refill}\]

\[Pond\_Overflow(t)=\max\left( \begin{array}{@{}ll@{}} 0 \\ (V(t-1) + Rain(t) * S0 / 1000. + RunOff(t) - Pond\_Irrigation(t) - Evaporation(t) - Percolation(t) + AvailableWater(t)) - V0 \end{array}\right) \label{eq:Pond_Overflow}\]

\[V(t) = V(t-1) + Rain(t) * S0 / 1000. + Runoff(t) + AvailableWater(t) - Pond\_Overflow(t) - Pond\_Irrigation(t) - Evaporation(t) - Percolation(t) \label{eq:V}\]
and initialized with : \(V(0) = Init\_Pond\_Frac * V0\)

\[Z(t) = Z0 - Z1 + \sqrt[3]{\frac{3 * (V(t) + V1)}{fx * fy}} \label{eq:Z}\]

\(X(t) = (Z(t) + Z1 - Z0) * fx\)
\(Y(t) = (Z(t) + Z1 - Z0) * fy\)
\(S(t) = X(t) * Y(t) = (Z(t) + Z1 - Z0)^2 * fx * fy\)
\(V(t) = \frac{1}{3} * S(t) * (Z(t) + Z1 - Z0) - V1 = \frac{1}{3} * (Z(t) + Z1 - Z0)^3 * fx * fy - V1\)
\((Z(t) + Z1 - Z0)^3 =\frac{3 * (V(t) + V1)}{fx * fy}\)

\[X(t) = (Z(t) + Z1 - Z0) * fx \label{eq:X}\]

\[Y(t) = (Z(t) + Z1 - Z0) * fy \label{eq:Y}\]

\[S(t) = X(t) * Y(t) = (Z(t) + Z1 - Z0)^2 * fx * fy \label{eq:S}\]

Atomic model IrrigationPriority

The IrrigationPriority model (using extension class DiscreteTimeDyn) estimate the priority for irrigation among the different plots of the farm. It is computed for each crops of each plots. The lowest value of IrrigationPriority is the highest priority.

Configuring a IrrigationPriority Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : IrrigationPriority

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
nbBele	int	[x]	number of plots to manage
a	double	[x]	strategy weight coefficient for plot priority
b	double	[x]	strategy weight coefficient for crop water stress
c	double	[x]	strategy weight coefficient for crop cycle completeness
d	double	[x]	strategy weight coefficient for irrigation technics
RS_strategy	int	[x]	Ranking Stress strategy, {1:favor most stressed ; 2:favor least stressed}
RC_strategy	int	[x]	Ranking Cycle strategy, {1:favor latest in crop cycle ; 2:favor earliest in crop cycle}
BelePriorities	set < double >	[x]	Ranking of the different plots, all values must be different from each others

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

CropPriority_i : crop priority related to economic factor and crop cycle length (-) (double) (sync)
Days_Without_Irrigation_i : number of consecutive days with no irrigation where it should have for plot i with i ∈ [1, nbBele] (days) (double) (nosync)
Lethal_Threshold_Days_Without_Water_i : number of days of water deficit after which the crop is failed for plot i with i ∈ [1, nbBele] (days) (double) (sync)
Days_Since_Sowing_i : number of days since sowing for plot i with i ∈ [1, nbBele] (days) (double) (nosync)
Crop_Cycle_Duration_i : total expected crop cycle for plot i with i ∈ [1, nbBele] (days) (double) (sync)
Irrigation_Technic_Factor_i : irrigation technic factor (from least to most demanding in water) for plot i with i ∈ [1, nbBele] (-) (double) (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

IrrigationPriority_i : Priority order (going from 1 to nbBele) of plot i with i ∈ [1, nbBele] (-) [int]
R_i : Priority factor of plot i with i ∈ [1, nbBele] (-) [double]
RE_i : Ranking Economy of plot i with i ∈ [1, nbBele] (-) [double]
RS_i : Ranking Stress of plot i with i ∈ [1, nbBele] (-) [double]
RC_i : Ranking Cycle of plot i with i ∈ [1, nbBele] (-) [double]
RT_i : Ranking Technics of plot i with i ∈ [1, nbBele] (-) [double]

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/IrrigationPriority : set all parameters with default values

Details

State variables equations

RE (Ranking Economy) : Plot priority related to economic factors (investments, market prices, …) and crop cycle duration (also related to economic factors as most of the time long cycles are more investment demanding). The idea is to rank all crops used. ∈ [0, 1] \[RE\_i(t)= \frac{CropPriority\_i(t)}{sum_i(CropPriority\_i(t))} \label{eq:RE}\]

RS (Ranking Stress) : factor related to accumulated crop stress (number of days without irrigation). 2 strategies are possible : (i) favor the most stressed crops to avoid failure, or (ii) favor the least stressed crops, because the most stressed ones have disminished their potential yield. ∈ [0, 1] \[ RS\_i(t)=\left\{ \begin{array}{@{}ll@{}} \frac{Lethal\_Threshold\_Days\_Without\_Water\_i(t) - Days\_Without\_Irrigation\_i(t-1)}{Lethal\_Threshold\_Days\_Without\_Water\_i(t)}, & \text{if}\ RS\_strategy=1 \\ \frac{Days\_Without\_Irrigation\_i(t-1)}{Lethal\_Threshold\_Days\_Without\_Water\_i(t)}, & \text{else if}\ RS\_strategy=2 \\ \end{array}\right. \label{eq:RS}\]

RC (Ranking Cycle) : factor related to relative normalised crop cycle realisation. 2 strategies are possible : (i) favor the crops closest to the end of their cycle to ensure harvest, or (ii) favor crops at the begining of their cycle to ensure correct development during early stages. ∈ [0, 1] \[ RC\_i(t)=\left\{ \begin{array}{@{}ll@{}} \frac{Crop\_Cycle\_Duration\_i(t) - Days\_Since\_Sowing\_i(t-1)}{Crop\_Cycle\_Duration\_i(t)}, & \text{if}\ RC\_strategy=1 \\ \frac{Days\_Since\_Sowing\_i(t-1)}{Crop\_Cycle\_Duration\_i(t)}, & \text{else if}\ RC\_strategy=2 \\ \end{array}\right. \label{eq:RC}\]

RT (Ranking Technics) : factor related to the irrigation technic (drip, sprinkler, furrow, …). Rank crops by their irrigation technics from the least demanding in water to the most ones. ∈ [0, 1] \[RT\_i(t)= \frac{Irrigation\_Technic\_Factor\_i(t)}{max_i(Irrigation\_Technic\_Factor\_i(t))} \label{eq:RT}\]

\[R\_i(t)= a * RE\_i(t) + b * RS\_i(t) + c * RC\_i(t) + d * RT\_i(t) \label{eq:R}\]

IrrigationPriority_i(t) : rank of ascending ordered values of R_i(t), for ex-aequo values of R_i(t) the lowest value of BelePriorities is first

Atomic model FarmIrrigationManager

The FarmIrrigationManager model (using extension class DiscreteTimeDyn) estimate ….
All irrigation water is provided for plots on the first day but can be removed from pump or pond during several consecutive days of a water cycle

Configuring a FarmIrrigationManager Model

Dynamics settings

To define the dynamic:

library : ASCROM
name : FarmIrrigationManager

Parameters settings

List and information about all possible parameters (name, type, ismandatory, description with default value).

See documentation of DiscreteTimeDyn to get all available extension parameters (for example time_step)

Parameter name	Type	Is mandatory?	Description
DbgLog	double	[] (default=0)	Debug messages verbosity level
nbBele	int	[x]	number of plots to manage
isPondForIrrigation	bool	[x]	define if pond water can be used for irrigation
isOptimize	bool	[x]	define if water from last day of a cycle can be used (see case 2.1)
isRefill	bool	[x]	define if water from pump can be used to refill the pond
V0	double	[x]	pond total volume (m³)
PlotArea_i	double	[x]	plot area of the plot i with i ∈ [1, nbBele] (m²)

Input settings

List and information about all possible input ports (name, type, description with units).

for model using extension discrete-time also include sync info

V : Pond water volume (m³) (double) (nosync)
AvailableWater : pump maximum available water (m³.d^-1) (double) (sync)
PumpMaxVol : maximum water volume reachable by the pump (m³ of water) (double) (sync)
IrrigationDemand_i : daily irrigation demand of plot i with i ∈ [1, nbBele] (mm.d^-1) (double) (sync)
Max_Irrigation_Duration_i : Maximal water cycle duration for plot i with i ∈ [1, nbBele] (days) (double) (sync)
IrrigationPriority_i : Priority order (going from 1 to nbBele) of plot i with i ∈ [1, nbBele] (-) [int] (sync)

Output settings

List and information about all possible output ports (name, type, description with units).

PondExtraction : daily actual irrigation using pond water (m³) (double)
PumpExtraction : daily actual water pumped (m³) (double)
PondRefill : water for refilling the pond (m³) (double)
WaterCycle_Duration : remaining duration of active water cycle (int) (double)
WaterCycle_RemainingAmount : remaining water amount of active water cycle (m³) (double)
WaterCycle_CurrentPlot : plot index of active water cycle (int) (double)
WaterCycle_CurrentDose : daily pumping water of active water cycle (m³) (double)
IrrigationAmount_i : daily actual irrigation for plot i with i ∈ [1, nbBele] (m³) (double)
Irrigation_i : daily actual irrigation for plot i with i ∈ [1, nbBele] (mm.d^-1) (double)
Is_Day_Without_Irrigation_i : detect if day has no irrigation where it should have for plot i with i ∈ [1, nbBele] (bool) (double)
Days_Without_Irrigation_i : number of consecutive days with no irrigation where it should have for plot i with i ∈ [1, nbBele] (days) (double)
PondExtraction_i : daily actual irrigation using pond water for plot i with i ∈ [1, nbBele] (m³) (double)
PumpExtraction_i : daily actual water pumped for plot i with i ∈ [1, nbBele] (m³) (double)

Observation settings

List and information about all possible observation ports (name, type, description with units).

Same as Output settings, see above.

Available configurations

List and information about all configuration metadata files

ASCROM/FarmIrrigationManager : set all parameters with default values

Details

State variables equations

Some state variables use different equations depending on the following cases and sub-cases :
1. Current day is not in an active water cycle
  1.1. No plot request any water
  1.2. At least one plot request water
2. Current day is in an active water cycle

Local variables defined and used in the following part are initialized as :

\[ pond\_AvailableIrrigationWater=\left\{ \begin{array}{@{}ll@{}} V(-1), & \text{if}\ isPondForIrrigation(t) \\ 0, & \text{otherwise}\ \\ \end{array}\right. \label{eq:pond_AvailableIrrigationWater_1_2_init}\]

\[pump\_AvailableIrrigationWater = AvailableWater(t) \label{eq:pump_AvailableIrrigationWater_1_2_init}\]

\[total\_AvailableIrrigationWater = pond\_AvailableIrrigationWater + pump\_AvailableIrrigationWater \label{eq:total_AvailableIrrigationWater_1_2_init}\]

\[pond\_extraction = 0 \label{eq:pond_extraction_1_2_init}\]

\[pump\_extraction = 0 \label{eq:pump_extraction_1_2_init}\]

\[cycle\_max\_amount = PumpMaxVol(t) + pond\_AvailableIrrigationWater \label{eq:cycle_max_amount_1_2_init}\]

For each plot the local variables defined and used in the following part are initialized as :

\[plot\_irrig\_demand\_i = IrrigationDemand\_i(t) * PlotArea\_i / 1000. \label{eq:plot_irrig_demand_1_2_init}\] ∀ i ∈ [1, nbBele]

\[plot\_cycle\_duration\_i = ceil(\frac{plot\_irrig\_demand\_i - total\_AvailableIrrigationWater}{AvailableWater(t)}) \label{eq:plot_cycle_duration_1_2_init}\] ∀ i ∈ [1, nbBele]

Case 1.1 : Current day is not in an active water cycle and No plot request any water

Case detection : if \((WaterCycle\_Duration(t-1) <= 0.)\) & \((sum_i(IrrigationDemand\_i(t))==0)\)

Local variables equations :

\[pond\_extraction = 0 \label{eq:PondExtraction_1_1}\]

\[pump\_extraction = 0 \label{eq:PumpExtraction_1_1}\]

State Variables equations :

\[WaterCycle\_Duration(t) = 0 \label{eq:WaterCycle_Duration_1_1}\]

\[WaterCycle\_RemainingAmount(t) = 0 \label{eq:WaterCycle_RemainingAmount_1_1}\]

\[WaterCycle\_CurrentPlot(t) = -1 \label{eq:WaterCycle_CurrentPlot_1_1}\]

\[WaterCycle\_CurrentDose(t) = 0 \label{eq:WaterCycle_CurrentDose_1_1}\]

\[IrrigationAmount\_i(t) = 0 \label{eq:IrrigationAmount_1_1}\] ∀ i ∈ [1, nbBele]

\[Is\_Day\_Without\_Irrigation\_i(t) = 0 \label{eq:Is_Day_Without_Irrigation_1_1}\] ∀ i ∈ [1, nbBele]

Case 1.2 : Current day is not in an active water cycle and at least one plot request water

Case detection : if \((WaterCycle\_Duration(t-1) <= 0.)\) & \((sum_i(IrrigationDemand\_i(t))>0)\)

Sequential loop over all plots requesting water using increasing values of IrrigationPriority_i(t), for each plot 3 cases are possible :

1.2.1. All the requested water can be provided in a single day using the pump and pond.
1.2.2 All the requested water can be provided during a water cycle.
1.2.3 Not all the requested water can be provided neither in a single day nor during a water cycle.

Case 1.2.1 All the requested water can be provided in a single day using the pump and pond.

Case detection : if \((WaterCycle\_Duration(t) <= 0.)\) & \((plot\_irrig\_demand\_i <= total\_AvailableIrrigationWater)\)

Local variables equations :

\[pond\_AvailableIrrigationWater = pond\_AvailableIrrigationWater - pond\_flow \label{eq:pond_AvailableIrrigationWater_1_2_1}\]
with
\(pond\_flow =\min\left( \begin{array}{@{}ll@{}} pond\_AvailableIrrigationWater \\ plot\_irrig\_demand\_i \end{array}\right)\)

\[pump\_AvailableIrrigationWater = pump\_AvailableIrrigationWater - pump\_flow \label{eq:pump_AvailableIrrigationWater_1_2_1}\]
with
\(pump\_flow =plot\_irrig\_demand\_i - \min\left( \begin{array}{@{}ll@{}} pond\_AvailableIrrigationWater \\ plot\_irrig\_demand\_i \end{array}\right)\)

\[pond\_extraction = pond\_extraction + pond\_flow \label{eq:pond_extraction_1_2_1}\]

\[pump\_extraction = pump\_extraction + pump\_flow \label{eq:pump_extraction_1_2_1}\]

\[total\_AvailableIrrigationWater = pond\_AvailableIrrigationWater + pump\_AvailableIrrigationWater \label{eq:total_AvailableIrrigationWater_1_2_1}\]

\[cycle\_max\_amount = PumpMaxVol(t) - pump\_extraction + pond\_AvailableIrrigationWater \label{eq:cycle_max_amount_1_2_1}\]

State Variables equations :

\[IrrigationAmount\_i(t) = plot\_irrig\_demand\_i \label{eq:IrrigationAmount_1_2_1}\]

\[Is\_Day\_Without\_Irrigation\_i(t) = 0 \label{eq:Is_Day_Without_Irrigation_1_2_1}\]

Case 1.2.2 All the requested water can be provided during a water cycle.

Case detection : if \(( WaterCycle\_Duration(t)==0. )\) & \(( plot\_irrig\_demand\_i <= cycle\_max\_amount )\) & \(( plot\_cycle\_duration\_i <= Max\_Irrigation\_Duration\_i(t) )\)

Local variables equations :

\[pond\_extraction = pond\_extraction + pond\_AvailableIrrigationWater \label{eq:pond_extraction_1_2_2}\]

\[pump\_extraction = pump\_extraction + pump\_AvailableIrrigationWater \label{eq:pump_extraction_1_2_2}\]

\[pond\_AvailableIrrigationWater = 0 \label{eq:pond_AvailableIrrigationWater_1_2_2}\]

\[pump\_AvailableIrrigationWater = 0 \label{eq:pump_AvailableIrrigationWater_1_2_2}\]

\[total\_AvailableIrrigationWater = pond\_AvailableIrrigationWater + pump\_AvailableIrrigationWater \label{eq:total_AvailableIrrigationWater_1_2_2}\]

\[cycle\_max\_amount = PumpMaxVol(t) - pump\_extraction + pond\_AvailableIrrigationWater - (plot\_irrig\_demand\_i - total\_AvailableIrrigationWater) \label{eq:cycle_max_amount_1_2_2}\]

State Variables equations :

\[WaterCycle\_Duration(t) = plot\_cycle\_duration\_i \label{eq:WaterCycle_Duration_1_2_2}\]

\[WaterCycle\_RemainingAmount(t) = plot\_irrig\_demand\_i - total\_AvailableIrrigationWater \label{eq:WaterCycle_RemainingAmount_1_2_2}\]

\[WaterCycle\_CurrentPlot(t) = i \label{eq:WaterCycle_CurrentPlot_1_2_2}\]

\[WaterCycle\_CurrentDose(t) = AvailableWater(t) \label{eq:WaterCycle_CurrentDose_1_2_2}\]

\[IrrigationAmount\_i(t) = plot\_irrig\_demand\_i \label{eq:IrrigationAmount_1_2_2}\]

\[Is\_Day\_Without\_Irrigation\_i(t) = 0 \label{eq:Is_Day_Without_Irrigation_1_2_2}\]

Case 1.2.3 Not all the requested water can be provided neither in a single day nor during a water cycle.

Case detection : otherwise

\[IrrigationAmount\_i(t) = 0 \label{eq:IrrigationAmount_1_2_3}\]

\[Is\_Day\_Without\_Irrigation\_i(t) = 1 \label{eq:Is_Day_Without_Irrigation_1_2_3}\]

Case 2 : Current day is in an active water cycle

Case detection : if \((WaterCycle\_Duration(t-1) > 0.)\)

\[WaterCycle\_Duration(t) = WaterCycle\_Duration(t-1) - 1 \label{eq:WaterCycle_Duration_2}\]

\[WaterCycle\_RemainingAmount(t)=\max\left( \begin{array}{@{}ll@{}} 0 \\ WaterCycle\_RemainingAmount(t-1) - WaterCycle\_CurrentDose(t) \end{array}\right) \label{eq:WaterCycle_RemainingAmount_2}\nonumber\]

\[ WaterCycle\_CurrentPlot(t)=\left\{ \begin{array}{@{}ll@{}} WaterCycle\_CurrentPlot(-1), & \text{if}\ WaterCycle\_Duration(t)!=0 \\ -1, & \text{otherwise}\ \\ \end{array}\right. \label{eq:WaterCycle_CurrentPlot_2}\]

\[ WaterCycle\_CurrentDose(t)=\left\{ \begin{array}{@{}ll@{}} WaterCycle\_CurrentDose(-1), & \text{if}\ WaterCycle\_Duration(t)!=0 \\ 0, & \text{otherwise}\ \\ \end{array}\right. \label{eq:WaterCycle_CurrentDose_2}\]

\[pond\_extraction = 0 \label{eq:PondExtraction_2}\]

\[pump\_extraction=\min\left( \begin{array}{@{}ll@{}} WaterCycle\_CurrentDose(t) \\ WaterCycle\_RemainingAmount(t-1) \end{array}\right) \label{eq:PumpExtraction_2}\nonumber\]

\[IrrigationAmount\_i(t) = 0 \label{eq:IrrigationAmount_2}\] ∀ i ∈ [1, nbBele]

\[ Is\_Day\_Without\_Irrigation\_i(t)=1 \label{eq:Is_Day_Without_Irrigation_2}\] ∀ i ∈ [1, nbBele]

Case 2.1 : Current day is the last day of an active water cycle

If isOptimize option is activated.

In the case where it is the last day of an active water cycle we subsequently try to do 1 day irrigations (similar to case 1.2.1), using the remaining water and using pump volumes from the start of the water cycle.

Sequential loop over all plots requesting water using increasing values of IrrigationPriority_i(t).

Local variables defined and used in the following part are initialized as :

\[ pond\_AvailableIrrigationWater=\left\{ \begin{array}{@{}ll@{}} V(-1), & \text{if}\ isPondForIrrigation(t) \\ 0, & \text{otherwise}\ \\ \end{array}\right. \label{eq:pond_AvailableIrrigationWater_2_1_init}\]

\[pump\_AvailableIrrigationWater = WaterCycle\_CurrentDose(t-1) - WaterCycle\_RemainingAmount(t-1) \label{eq:pump_AvailableIrrigationWater_2_1_init}\]

\[total\_AvailableIrrigationWater = pond\_AvailableIrrigationWater + pump\_AvailableIrrigationWater \label{eq:total_AvailableIrrigationWater_2_1_init}\]

\[pond\_extraction = PondExtraction(t) \label{eq:pond_extraction_2_1_init}\]

\[pump\_extraction = PumpExtraction(t) \label{eq:pump_extraction_2_1_init}\]

For each plot the local variables defined and used in the following part are initialized as :

\[plot\_irrig\_demand\_i = IrrigationDemand\_i(t) * PlotArea\_i / 1000. \label{eq:plot_irrig_demand_2_1}\] ∀ i ∈ [1, nbBele]

if \((plot\_irrig\_demand\_i <= total\_AvailableIrrigationWater)\)

Local variables equations :

\[pond\_AvailableIrrigationWater = pond\_AvailableIrrigationWater - pond\_flow \label{eq:pond_AvailableIrrigationWater_2_1}\]
with
\(pond\_flow =\min\left( \begin{array}{@{}ll@{}} pond\_AvailableIrrigationWater \\ plot\_irrig\_demand\_i \end{array}\right)\)

\[pump\_AvailableIrrigationWater = pump\_AvailableIrrigationWater - pump\_flow \label{eq:pump_AvailableIrrigationWater_2_1}\]
with
\(pump\_flow =plot\_irrig\_demand\_i - \min\left( \begin{array}{@{}ll@{}} pond\_AvailableIrrigationWater \\ plot\_irrig\_demand\_i \end{array}\right)\)

\[pond\_extraction = pond\_extraction + pond\_flow \label{eq:pond_extraction_2_1}\]

\[pump\_extraction = pump\_extraction + pump\_flow \label{eq:pump_extraction_2_1}\]

\[total\_AvailableIrrigationWater = pond\_AvailableIrrigationWater + pump\_AvailableIrrigationWater \label{eq:total_AvailableIrrigationWater_2_1}\]
State Variables equations :

\[IrrigationAmount\_i(t) = plot\_irrig\_demand\_i \label{eq:IrrigationAmount_2_1}\]

\[Is\_Day\_Without\_Irrigation\_i(t) = 0 \label{eq:Is_Day_Without_Irrigation_2_1}\]

State variable that use a single equation (computed at the end of daily loop) :

Irrigation_i with i ∈ [1, nbBele] (mm.d^-1) unit conversion from (m³) \[Irrigation\_i(t)= \frac{IrrigationAmount\_i(t) * 1000.}{PlotArea\_i} \label{eq:Irrigation_i}\] ∀ i ∈ [1, nbBele]

Days_Without_Irrigation_i with i ∈ [1, nbBele] (day) counter of consecutive days where Is_Day_Without_Irrigation_i \[ Days\_Without\_Irrigation\_i(t)=\left\{ \begin{array}{@{}ll@{}} Days\_Without\_Irrigation\_i(t-1) + 1, & \text{if}\ Is\_Day\_Without\_Irrigation\_i(t)=1 \\ 0, & \text{otherwise}\ \\ \end{array}\right. \label{eq:Days_Without_Irrigation}\] ∀ i ∈ [1, nbBele]

\[PondRefill(t)=\left\{ \begin{array}{@{}ll@{}} \min\left( \begin{array}{@{}ll@{}} pump\_AvailableIrrigationWater \\ V0 - V(t-1) \end{array}\right), & \text{if}\ isRefill \\ 0, & \text{otherwise}\ \\ \end{array}\right. \label{eq:PondRefill}\] along with \(pump\_extraction = pump\_extraction + PondRefill(t)\)

\[PondExtraction(t)=pond\_extraction \label{eq:PondExtraction}\]

\[PumpExtraction(t)=pump\_extraction \label{eq:PumpExtraction}\]

Annexes

Tables

Table 1: Kc (extract of FAO)

Table 2: fw

Table 3: fc

Table4: REW REW

Table 5: Crop stage duration, by climate

ASCROM package documentation

Package ASCROM for vle-2.0.2

Table of Contents

Package dependencies

Atomic model ClimaticWaterDemand

Configuring a ClimaticWaterDemand Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Calculation of Kcb

Calculation of Ke

Atomic model WaterFlows

Configuring a WaterFlows Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Atomic model IrrigationDemand

Configuring a IrrigationDemand Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Rule_Strat=Rain_Threshold

Rule_Strat=SoilWaterContent_Threshold

Rule_Strat=CropWaterStress_Threshold

Atomic model ActualIrrigation

Configuring a ActualIrrigation Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Atomic model Yield

Configuring a Yield Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Atomic model Pond

Configuring a Pond Model

Dynamics settings

Parameters settings

Local parameters

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations

Atomic model IrrigationPriority

Configuring a IrrigationPriority Model

Dynamics settings

Parameters settings

Input settings

Output settings

Observation settings

Available configurations

Details

State variables equations